multiview¶
The multiview module consists of:
- a collection of solvers for 2 to n-view geometry constraints that arise in multiple view geometry,
- a generic framework “Kernel” that can embed these solvers for robust estimation.
First accessible solvers are listed and explained and the “Kernel” concept is documented.
2-view solvers (2d-2d correspondences)¶
openMVG provides solver for the following geometric estimation:
- affine,
- homographic,
- fundamental,
- 7 to n pt,
- 8 to n pt (Direct Linear Transform) [HZ].
- essential,
- 8 to n pt (Direct Linear Transform) [HZ],
- 5pt + intrinsic [Stewenius], [Nister].
N-View geometry estimation¶
- Triangulation
- 2 to n view (Direct Linear Transform),
- 2 to n view (Iterated least square).
- Rotation averaging
- L2 (sparse) [Martinec],
- L1 (sparse) [Chatterjee].
- Translation averaging
- L2 Chordal [Kyle2014],
- SoftL1 ‘approximation of the LInf method of [GlobalACSfM]‘.
Homography matrix:¶
The homography matrix maps the relation between two projections of a plane: Figure.
\(H\) is a (3 x 3) matrix that links coordinates in left and right images with the following relation.
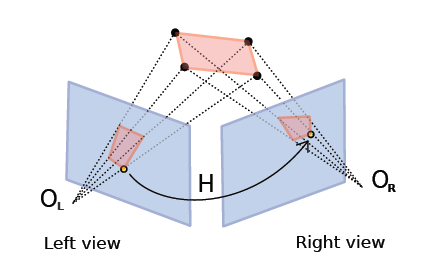
The homography matrix and the point to point constraint.
OpenMVG implementation follows the DLT (Direct Linear Transform) explained in [HZ] book: \(H\) can be estimated from 4 to \(n\) corresponding points.
Fundamental matrix:¶
The fundamental matrix is a relation between two images viewing the same scene where those point’s projections are visible in the two images. Given a point correspondence between two views \((x_i,x'_i)\):
We obtain the following relation:
\(F\) is the (3 x 3) Fundamental matrix, it puts in relation a point x to a line where belong the projection of the 3D X point. \(l'_i = Fx_i\) designs the epipolar line on which the point \(x'_i\) could be. The relation \(x'^T_i Fx_i = 0\) exists for all corresponding point belonging to a stereo pair.
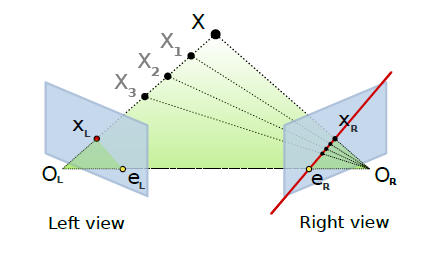
The fundamental matrix and the point to line constraint.
The fundamental matrix is sometime called bifocal-tensor, it is a 3 x 3 matrix of rank 2 with 7 degree of freedom. 8 ou 7 correspondences are sufficient to compute the \(F\) matrix. Implementation follows the DLT (Direct Linear Transform) explained in [HZ] book.
Relative pose estimation (Essential matrix)¶
Adding intrinsic parameters to the fundamental matrix gives a metric “object” that provides the following relation \(E = K'^T FK\) , this is the Essential relation explained by Longuet-Higgins in 1981 [Longuet]. This essential matrix links the relative position of the camera to the fundamental matrix relation.
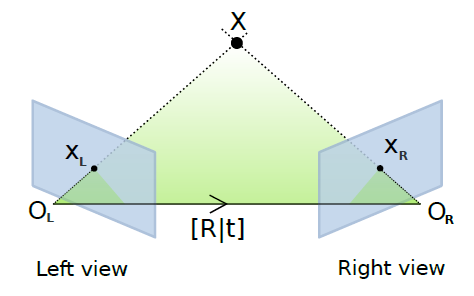
The essential matrix geometric relation.
Absolute pose estimation/Camera resection (Pose matrix)¶
Given a list of 3D-2D point correspondences it is possible to compute a camera pose estimation. It consists in estimating the camera parameters of the right camera that minimizes the residual error of the 3D points re-projections, it’s an optimization problem that trying to solve P parameters in order to minimize
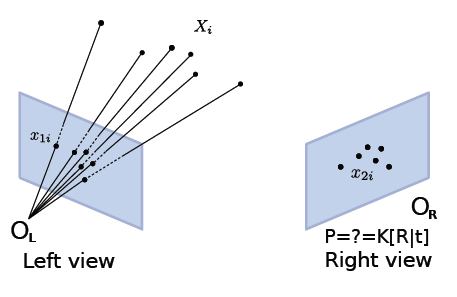
Resection/Pose estimation from 3D-2D correspondences.
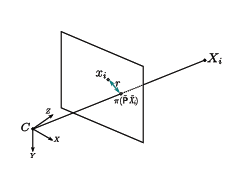
Residual error.
openMVG provides 3 different solvers for this problem:
Kernel concept¶
In order to use the solver in a generic robust estimation framework, we use them in conjuction with the Kernel class that allow to link:
- data points,
- the set of correspondences that are used for a robust estimation problem.
- a model solver/estimator,
- a metric to measure data fitting to a putative model.
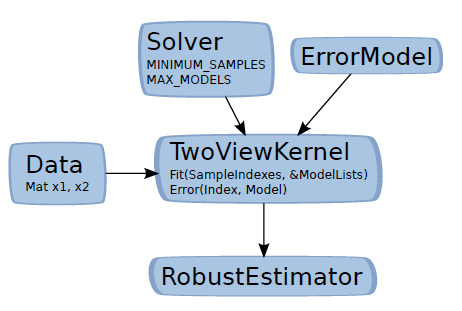
The Kernel concept (the two view case).
- Solver:
- MINIMUM_SAMPLES: The minimal number of point required for the model estimation, MAX_MODELS: The number of models that the minimal solver could return, A Solve function that estimates a model from MINIMUM_SAMPLES to n vector data.
- ErrorModel:
- An metric function that return the error of a sample data to the provided model.
- Kernel:
- Embed data (putative), the model estimator and the error model. This kernel is core brick used in the openMVG robust estimator framework.