robust_estimation¶
Performing model estimation is not an easy task, data are always corrupted by noise and “false/outlier” data so robust estimation is required to find the “best” model along the possible ones.
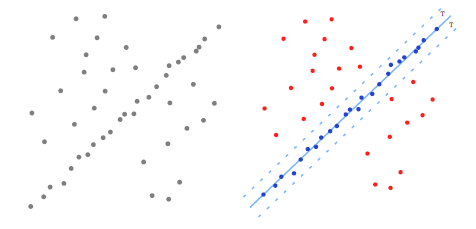
Robust estimation: Looking for a line in corrupted data.
openMVG provides many methods to estimate one of the best possible model in corrupted data:
- Max-Consensus,
- Ransac,
- LMeds,
- AC-Ransac (A Contrario Ransac).
Max-Consensus¶
The idea of Max-Consensus is to use a random picked subset of data to find a model and test if this model is good or not the whole dataset. At the end you keep the model that best fits your cost function. Best fit defined as the number of data correspondences to the model under your specified threshold T.
Algorithm 1 Max-Consensus
Require: correspondences
Require: model solver, residual error computation
Require: T threshold for inlier/outlier discrimination
Require: maxIter the number of performed model estimation
Ensure: inlier list
Ensure: best estimated model Mbest
for i = 0 ! maxIter do
Pick NSample random samples
Evaluate the model Mi for the random samples
Compute residuals for the estimated model
if Cardinal(residual < T) > previousInlierCount then
previousInlierCount = Cardinal(residual < T)
Mbest = Mi
end if
end for
Here an example of how find a best fit line:
Mat2X xy ( 2 , 5);
// Defines some data points
xy << 1, 2, 3, 4, 5, // x
3, 5, 7, 9, 11; // y
// The base model estimator and associated error metric
LineKernel kernel ( xy );
// Call the Max-Consensus routine
std::vector<uint32_t> vec_inliers;
Vec2 model = MaxConsensus ( kernel , ScorerEvaluator<LineKernel >(0.3) , &-vec_inliers );
Ransac¶
Ransac [RANSAC] is an evolution of Max-Consensus with a-priori information about the noise and corrupted data amount of the data. That information allows to reduce the number of iterations in order to be sure to have made sufficient random sampling steps in order to find the model for the given data confidence. The number of remaining steps is so iteratively updated given the inlier/outlier ratio of the current found model.
Here an example of how find a best fit line:
Mat2X xy ( 2 , 5);
// Defines some data points
xy << 1, 2, 3, 4, 5, // x
3, 5, 7, 9, 11; // y
// The base model estimator and associated error metric
LineKernel kernel ( xy );
// Call the Ransac routine
std::vector<uint32_t> vec_inliers;
Vec2 model = Ransac ( kernel, ScorerEvaluator<LineKernel >(0.3) , &vec_inliers );
AC-Ransac A Contrario Ransac¶
RANSAC requires the choice of a threshold T, which must be balanced:
- Too small: Too few inliers, leading to model imprecision,
- Too large: Models are contaminated by outliers (false data).
AC-Ransac [ACRANSAC] uses the a contrario methodology in order to find a model that best fits the data with a confidence threshold T that adapts automatically to noise. It so finds a model and its associated noise. If there is too much noise, the a contrario method returns that no model was found.
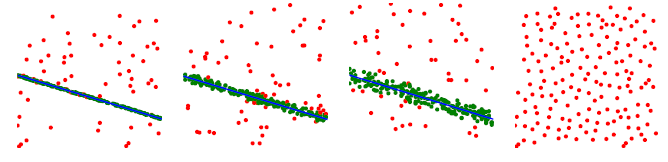
A contrario robust estimation, noise adaptivity.
Here an example of how to find a best fit line, by using the a contrario robust estimation framework: It is a bit more complex, we use a class in order to perform the a contrario required task.
Mat2X xy ( 2 , 5);
// Defines some data points
xy << 1, 2, 3, 4, 5, // x
3, 5, 7, 9, 11; // y
// The acontrario adapted base model estimator and associated error metric
const size_t img_width = 12;
ACRANSACOneViewKernel<LineSolver, pointToLineError, Vec2> lineKernel(xy, -img_width, img_width);
// Call the AC-Ransac routine
std::vector<uint32_t> vec_inliers;
Vec2 line;
std::pair<double, double> res = ACRANSAC(lineKernel, vec_inliers, 300, &line);
double dPrecision = res.first;
double dNfa = res.second;